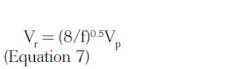Quiescent Settling
With quiescent settling, the relevant design parameter is the volume of the wet pool rather than its surface area. This is understood intuitively. The larger the volume of the wet pool in relationship to the incoming storm volume, the greater the fraction of the storm volume retained by the basin, and in turn, the greater the percentage of the settleable solids retained for settling during the quiescent period. This relationship in its simplest form is described for a wet basin by Equation 6.
Equation 6 indicates that the fraction of particles removed depends on the fraction of inflow volume retained by the settling basin. Stated differently, it represents the fraction of particles present in the event volume that is retained by the basin. If the settling time for the particle of interest is less than the time to the next event, all of the solids of that size or smaller will reach the bottom before the next event.
However, if the settling time for the particle of interest is greater than the time to the next event, only a fraction of the particles trapped in the basin will reach the bottom.
Equation 6 assumes ideal hydraulic conditions; that is, a complete exchange occurs between the volume of the incoming water and an equal volume present in the basin prior to the event. The equation says that basins that retain water between storms have a greater removal efficiency than basins that are dry between storms, if all other factors such as size and hydraulic efficiency are the same.
Factors Affecting the Relative Significance of Each
The comparison of the two settling periods, dynamic and quiescent, raises the question of which period is dominant in wet basins and therefore which design parameter, volume or surface area, is most relevant.
The relative importance of each type of settling is determined by whether the settling is discrete or flocculent, the settling velocity distribution of the particles in the stormwater, the volume of the basin relative to the volume of the storm, and the treatment efficiency goal.
If the suspension is discrete, surface area is more significant. If the suspension is flocculent, basin depth and therefore volume become significant. The greater the fraction of fine solids (with low settling velocities), the less significant the dynamic period, and the more significant the quiescent period. The issue of clays is relevant only when there is a significant amount of clay, say on the order of 10 to 20%.
Given that a significant percentage of settleable solids in stormwater are small and have low settling velocities, as well as that most stormwater suspensions appear to be flocculent, it is likely that volume is the more relevant design parameter. The greater the volume of the wet pool relative to the volume of the storms, the more significant the quiescent period.
If the desirable treatment efficiency is modest in the case of a pretreatment wet basin, the dynamic period becomes more significant. If the treatment efficiency goal is high in the case of a wet basin that serves as the primary unit operation, quiescent settling increases in importance.
It is commonly believed that wet basins should be sized based on a specified hydraulic residence time during the storm period. However, the above discussion establishes that hydraulic residence time during the storm is not a relevant design parameter, regardless of which settling period is dominant.
A more relevant hydraulic residence time is that between the storms, or the average annual hydraulic residence time. It represents the average time water resides in the wet basin over a year. The average hydraulic residence time provides an indication of the time available for settling during the quiescent period. It is the total annual runoff divided by the depth of the mean annual runoff event multiplied by 365 to give the units of days.
Resuspension
Resuspension of previously settled sediments or organic matter during extreme events is a concern in basins and swales. The condition may be exacerbated by narrowing basins to improve hydraulic efficiency, thereby increasing the longitudinal velocity. Except for wind, resuspension is likely to occur only in the inlet and outlet areas.
A study found little resuspension in a sedimentation basin with a depth of 3 feet (1 meter). The general guideline to keep sand from resuspending is to keep the water velocity below 1 foot per second (30 centimeters per second). Higher velocities are allowed for smaller particles, in the range of 50 to 100 microns or less, due to their cohesive nature. Because of their feeding habits, ducks and swans will cause resuspension of bottom sediments.
The force required to resuspend a particle is related to the force keeping it down, which in turn is related to the settling velocity of the particle and the cohesiveness between particles. Methods of analysis for calculating resuspension velocities are available from water and wastewater treatment engineering, river engineering, and mining engineering. Equation 7, drawn from water and wastewater treatment engineering, is applicable to low-density organic solids.Where:
Vr = resuspension water velocity
f = Darcy-Weisbach friction factor, taken as English: 0.025 units
Vp = settling velocity of the particle
Vp represents the original settling velocity of the particle that is not to be resuspended. Resuspension velocity, Vr, is the average forward water velocity through the basin that will cause resuspension. For example, assume a settling velocity of 0.1 foot (3 centimeters) per second for the particle of interest. The resuspension velocity is about 1.8 feet per second. Average forward velocity in an in-line wet basin during extreme events may reach this value in small vaults. The assumed settling velocity represents organic particles 100 to 300 microns.
Equation 7 does not recognize that depth affects the value of Vr, which decreases with decreasing water depth. As the equation was developed for water and wastewater settling basins with depths of 10 to 15 feet (3.3 to 5 meters), the resuspension velocity for the same particle in stormwater wet basins might be considerably lower than indicated by Equation 7.
Equation 7 assumes that Vr decreases as particle size decreases through the entire size spectrum. This is a reasonable assumption for organic sediments. However, with inorganic sediments, Vr decreases as the particle size decreases only to a diameter of about 200 microns.
With inorganic particles less than 200 microns, Vr increases rather than decreases due to increasing cohesiveness of the sediment. For example, at 10 microns the critical velocity is about twice that of a 200-micron particle, although, based on Stokes Law it ought to be about one-fifth. These observations suggest that clays and silts are not likely to be resuspended during extreme events, except near the inlet, to the extent that the cohesive condition of the sediments are reestablished.
A field study of resuspension of deposited silts and clays in mine tailing ponds lead to Equation 8, which therefore may be most applicable to stormwater ponds and wetlands for inorganic sediments. The equation defines the minimum depth necessary to avoid resuspension by wind, not incoming water.
For a depth of 3 feet (1 meter), a pond of about 1,000 feet (330 meters) in the direction of the wind can withstand a wind velocity of 55 miles per hour (17 meters per second) before resuspension. According to this method, wetlands with depths less than 0.5 foot should experience resuspension of inorganic sediments if the basin length exceeds a few hundred feet. However, the effect should be moderated by the vegetation.
Resuspension by wind has been observed in wet ponds with depths less than 3 feet (1 meter). Bacteria in the water column ponds were observed to increase in the presence of wind, implying resuspension of sediments. Various equations for estimating resuspension potential have been studied. Other relationships have been developed on this topic.